Please do not reply to this Newsletter. You will likely get a response from a machine, not Nancy! For
feedback on the Newsletter or to correspond with Nancy, click here instead.
Magnetic Disruption
On July 15, 1995, at the start of ZetaTalk, the Zetas stated that the weakening magnetic field was
caused by the approach of Planet X. This early ZetaTalk was in response to a question about "base
resonant frequency" and how this technique showed the Earth's electrical field was weakening. Per the
Zetas, not weakening, but dispersing, confused and pulled in different directions by the presence of
Planet X.
ZetaTalk Claim 7/15/1995: Where some scientists state that the Earth's magnetic field has been
weakening lately, this is certainly not the case. They misunderstand. The Earth's magnetic field is
not weakening, it is changing course or direction, and thus scattered does not register on their
instruments in the same old way. This is an early indicator of the great confusion that Planet X
will have on the Earth, soon, during the pole shift. Another way to describe this dispersing is the
scientific term - base resonant frequency. This is just another name for magnetic pull, the
strength of the pull the Earth's core has on instruments. Instruments, through electricity coursing
through wires, create a magnetic field in a core of iron or some other highly susceptible material.
The resulting electromagnetic field can be either aligned with the Earth, or set to cross the
Earth's magnetic field, or at any partial angle that the scientists desire. Depending on the
strength of the Earth's own magnetic field, the field created by the instruments is thus disrupted
or weakened. This weakening disruption, noted by scientists, is just another indication of the
dispersal of the Earth's internal magnetic field.
The Zetas stated that Planet X was due to arrive in the inner solar system in 2003, which it did, tracked
carefully at the coordinates given by the Zetas during observatory observations, infrared sightings, and
CCD images as detailed on the ZetaTalk website. By March, 2003 it was visible as a red blur in the
evening sky to the right of Orion.
ZetaTalk Prediction 2/15/1996: When first sighted in 1983, it was on the right hand side of Orion,
as viewed from your northern hemisphere. It will first move left and up toward the elliptical
plane as it nears the Earth's Solar System for its passage, as though to assume a place with the
other planets in the Solar System, at this point being slightly to the left of Orion. In 1998 it will
veer right, moving toward Taurus and Aries, assuming a retrograde orbit, and will come up
through the plane as viewed from above the elliptical plane, in its first passage. Early on we
made clear what was about to happen, in 2003.
Curiously, an article published in the National Geographic on June 30, 2008 states that "rapid, almost
sudden" changes have taken place since 2003, the time when Planet X, per the Zetas in their early
predictions, arrived in the inner solar system.

- Earth's Core, Magnetic Field Changing Fast, Study Says
June 30, 2008
http://news.nationalgeographic.com/news/2008/06/080630-earth-core.html
- Rapid changes in the churning movement of Earth's liquid outer core are weakening the
magnetic field in some regions of the planet's surface. The findings suggest similarly quick
changes are simultaneously occurring in the liquid metal, 1,900 miles (3,000 kilometers)
below the surface. The swirling flow of molten iron and nickel around Earth's solid center
triggers an electrical current, which generates the planet's magnetic field. The study,
published recently in Nature Geoscience, modeled Earth's magnetic field using nine years
of highly accurate satellite data. In 2003 scientists found pronounced changes in the
magnetic field in the Australasian region. In 2004, however, the changes were focused on
Southern Africa.
Bank Failures
The subprime mortgage mess continues to ricochet throughout the banking industry. A Countrywide
baby, IndyMac Bank in California, has been closed by the Fed. Those depositors with savings of
$100,000 or less will be compensated by the Fed under FDIC rules. In classic bank closing panic,
depositors were withdrawing their funds at a rapid pace, while the bank was laying off half their
employees. Then the doors shut, suddenly, with only a notice on the front doors announcing the bank
had changed hands.

- IndyMac Bank Seized by Federal Regulators
July 12, 2008
http://www.latimes.com/business/la-fi-indymac12-2008jul12,0,6071779.story
- One woman leaned on the locked doors, pleading with an employee inside: "Please, please,
I want to take out a portion." All she could do was read a two-page notice taped to the
door. IndyMac's failure had been widely expected in recent days. As the bank was
shuttering offices and laying off employees to cope with huge losses from defaulted
mortgages made at the height of the housing boom, nervous depositors were pulling out
$100 million a day. The bank's stock price had plummeted to less than $1 as analysts
predicted the company's imminent demise. The takeover of IndyMac came amid rampant
speculation that the federal government would also have to take over lenders Fannie Mae
and Freddie Mac, which together stand behind almost half of the nation's mortgage debt.
There was no question that poor lending practices for home mortgages was responsible for the collapse
of IndyMac. It is certainly no surprise that to find an association with Countrywide.
- IndyMac Seized by U.S. Regulators Amid Cash Crunch
July 11, 2008
http://www.bloomberg.com/apps/news?pid=20601087&sid=atyF3ydPUlk8&refer=home
- The Pasadena, California-based lender specialized in so-called Alt-A mortgages, which
didn't require borrowers to provide documentation on their incomes. The lender racked up
almost $900 million in losses as home prices tumbled and foreclosures climbed to a record.
California ranked second among US states, with one foreclosure filing for every 192
households in June, 2.6 times the national average. The company was started in 1985 by
Countrywide founders.
The subprime mess is also affecting Wall Street, where the DOW is approaching 11,000, staggering
downward over continuing worries about bank stability.
- Paulson: No Bailout For Fannie Mae and Freddie Mac
July 11, 2008
http://www.huffingtonpost.com/2008/07/11/paulson-no-bailout-for-fa_n_112136.html
- Wall Street's angst over the ongoing fallout from the credit crisis made for a turbulent end
to a volatile week Friday _ stocks tumbled, soared and then turned south again as
investors tried to assess the dangers faced by the country's biggest mortgage financiers,
Fannie Mae and Freddie Mac. The fate of the government-chartered companies was a
focus of trading Friday as it had been earlier in the week. Shares of Fannie Mae and
Freddie Mac fell sharply over several sessions on concerns about their stability. Wall Street
is worried that a collapse of the two financiers would cause further shock to the financial
system, and trigger more losses to banks and brokerages with significant holdings of
mortgage-backed securities. The well-being of Fannie Mae and Freddie Mac is crucial
because they hold or guarantee about $5 trillion worth of mortgages, or about half the
outstanding mortgages in the United States. Their troubles are just the latest depressing
turn in a year-old credit crisis that shows no sign of ending.
The Zetas are asked almost weekly about the stability of the financial markets in the US and worldwide.
Will there be another collapse, such as occurred in 1929 during the Great Depression? Per the Zetas,
we are already there.
ZetaTalk Economic Analysis 4/5/2008: Wall Street knows that they are running a confidence
game, and thus all the talk about an "adjustment" taking place, and how this is a "good time to
buy", etc. If they were to admit the real economic reality they would be admitting that the US
and much of the world is in a depression, akin to the Great Depression of the 1930s. They are
hoping that you do not notice that the Emperor is not wearing clothes. Joblessness is high, with
employment numbers announced having no relationship to reality. New jobs are cooked up via a
mathematical formula called the "birth/death" formula, which assumes that if people are living
and breathing, they must be working. Those who use up their jobless claims are not included in
the rolls at all. Those who are drastically underemployed are likewise not included among the
jobless but among the employed. Corporate and personal bankruptcies and foreclosures are a
better indicator of the economy, as are flagging sales and corporate bottom lines. But you will
never hear officials or Wall Street admit that! To do so is to allow the public to finally begin
talking about the reality of what has been going on for years. And then what would they do?
Take responsibility?
The Zetas have consistently stated that the collapse of the dollar and the cost of food and gas will not
reach the point where the dollar is no longer used as a medium of exchange. The pole shift will occur
before this point. But the lessons learned during the Great Depression are being put into play, so the
banking industry will not be allowed to collapse. There may be price freezes, laws put into place to
prevent hoarding of foodstuffs, and limited banking hours along with withdrawal limits, but a complete
collapse of the dollar or the banking industry is not anticipated before the pole shift makes these matters
moot.
ZetaTalk Comment 6/28/2008: We have addressed the failing economy, failing worldwide, almost
every week. Nothing has changed, but our predictions have unfolded. We stated in 1995 when
ZetaTalk started that the Earth changes would cause economic distress. Crop failures, imploding
cities, flood ravaged lands - all of this reduces the standard of living and takes time and
resources. Businesses become distressed. Governments find it hard to collect taxes and care for
their citizenry. The behavior of the Bush administration was also predictable, with their invasion
of Iraq for the oil. Being aware of the pending passage, they bankrupt the US, without a care.
Now the dollar is dropping because of the Bush administration's incompetent management. This
impacts the price of everything within the US for the average US citizen. As we have been stating
regularly, it will get worse, and price freezes and limited banking hours may be imposed.
Eventually, per the Zetas, we will return to the barter system. This will occur gradually before the pole
shift but become the norm afterwards, worldwide. Per the Zetas, paper money such as dollars or stock
holdings or items such as jewelry or antiques or even gold will be worthless as they are simply a paper
promise and not a thing that can be delivered. Items such as seed, tools, land, fish hooks, flocks and
herds or skill sets will have value after the pole shift. These are items that can be used in barter.
ZetaTalk Comment 9/17/2004: The banking system or any paper money system is built on
confidence, confidence that a note will be paid out in something solid, something other than a
paper promise, which is what all money systems and bank notes are. Centuries past, when the
world was operating primarily on the barter system, such promises were few and were backed by
gold or silver, or land, or a herd of horses or cows, something solid. Villages and towns, farmers
and those in the trades, all operated primarily by barter, a cabinet built by a carpenter and
payment in a quarter of a slaughtered hog, a bushel of apples getting a tooth pulled by a dentist.
Financial sophistication developed slowly, based on the growing confidence that the backer of a
money system, a paper promise, could be counted upon to deliver something solid. Thus it was,
until recently, that gold was considered the backing. When the press to use paper money to
support a debtor economy ran beyond the supply of gold, the money systems were taken off the
gold standard. In the past, a creditor could put his house and property up as backing for a loan,
his herd, perhaps even his pending harvest of wheat, but could not get credit unless he had
something solid as collateral. But today it is the norm for every person, without substance to his
name, to have access to credit cards that allow him to go into debt beyond his ability to repay.
The creditor is given credit on the assumption that he will repay. The funds he is loaned are
assumed to have worth. And all pass paper promises around as though these were based on
things that could be brought forth upon demand.
Secklendorf Crop Circle
In the early days of ZetaTalk, the Zetas declined to decipher crop circles, telling mankind to gaze on the
crop circles and allow the subconscious to impart the message intended. But in 2004 they agreed to
explain the meaning of some crop circles, and one of the major themes was what the Zetas called
"magnetic trimesters." Many crop circles have three points or balls evenly placed around a circle, or a
triangle shape. Per the Zetas this is indicative of a magnetic influence affecting the solar system. The
summer trimester is the strongest, the fall trimester diminishing, and the spring trimester the most
quiescent.
ZetaTalk Explanation 7/6/2004: Summer Trimester (May-Aug): Normally a time when the
outburst is strongest. Fall Trimester (Sep-Dec): Normally a time when the annual outburst is
diminishing. Spring Trimester (Jan-Apr): Normally a quiet time when the outburst is quiescent,
just ahead of the yearly burst during the Summer Trimester.

These magnetic trimesters are indeed supported by HAARP documentation, as an examination of
magnetic signatures during the trimesters show. Recently the Zetas have stated that the pole shift will
occur at the end of a magnetic trimester, and have also stated that Earth changes will be most traumatic
during the summer trimester.
ZetaTalk Statement 6/14/2008: We have stated that the pole shift will occur at the end of a
magnetic trimester, which is the end of April, August, or December. We have stated that the
summer trimester has the most Earth changes. We have stated that the last weeks - 3 days of
darkness and all - will all occur within a magnetic trimester.
A recent crop circle laid in Germany on June 23, 2008 packs more information around the magnetic
trimesters, per the Zetas. Earth change incidence and planetary clash between Earth and her neighbors
during the trimesters leading into the time of the pole shift are shown, in relationship to the trimesters.
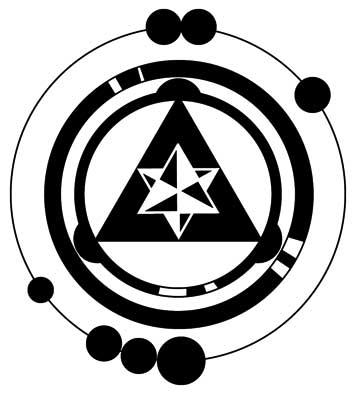
ZetaTalk Analysis 7/5/2008: The Secklendorf crop circle has merged many elements of the
coming pole shift. We have warned that the pole shift will occur toward the end of a magnetic
trimester, and the trimesters are clearly central to this design. The notched circles are indicative
of trauma points, with major trauma at the end of one trimester. Minor trauma is experienced
during the pole shift year during the other trimesters. What of the orbs in the outer circle? These
seem to be planets, of equal size in many instances, but what does the placement mean? Earth,
Venus, and the Dark Twin are of equal size. Earth and Venus are allowed to be crowded
together, caught in the cup, the eddy flow in front of Planet X as they are in separate orbits and
this puts distance between them. The third planet of equal size, the Dark Twin, is behind the
Earth in their shared orbit as the Repulsion Force keeps them apart. But what of the odd cluster
on the opposite side of the circle - planets of unequal size. Going into the pole shift, approaching
the end of the magnetic trimester when the pole shift will occur, there will be clashes between the
planets, including clashes with Planet X itself. As Planet X approaches the Earth, the cup of the
eddy flow tightens, forcing Earth and Venus toward Planet X, the larger orb, as it does so. The
Dark Twin falls outside of the cup at this point, thus becoming a minor element during the last
weeks.
Video Clip on Survivor Tips
 The Zeta Report 21 - Survivor Tips - So you've survived the pole shift. Now what? The Zeta Report 21 - Survivor Tips - So you've survived the pole shift. Now what?
Click on the image or click Here to watch.
You received this Newsletter because you subscribed to the ZetaTalk Newsletter service. If undesired, you can quickly
Unsubscribe.
|

